Spherical trigonometry is the branch of spherical geometry that deals with the relationships between trigonometric functions of the sides and angles of the spherical polygons (especially spherical triangles) defined by a number of intersecting great circles on the sphere. Spherical trigonometry is of great importance for calculations in astronomy, geodesy and navigation.
The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook Spherical trigonometry for the use of colleges and Schools. This book is now readily available on the web.[1] The only significant developments since then have been the application of vector methods for the derivation of the theorems and the use of computers to carry through lengthy calculations.
From this point the article will be restricted to spherical triangles, denoted simply as triangles.
The polar triangle associated with a triangle ABC is defined as
follows. Consider the great circle that contains the side BC. This great
circle is defined by the intersection of a diametral plane with the
surface. Draw the normal to that plane at the centre: it intersects the
surface at two points and the point that is on the same side of the
plane as A is (conventionally) termed the pole of A and it is denoted by
A'. The points B' and C' are defined similarly.
The triangle A'B'C' is the polar triangle corresponding to triangle ABC. A very important theorem (Todhunter,[1] Art.27) proves that the angles and sides of the polar triangle are given by
 and
and  etc.; see Spherical law of cosines.)
etc.; see Spherical law of cosines.)
Consider three unit vectors OA, OB and OC drawn from the origin to the vertices of the triangle (on the unit sphere). The arc BC subtends an angle of magnitude a at the centre and therefore OB·OC=cos a. Introduce a Cartesian basis with OA along the z-axis and OB in the xz-plane making an angle c with the z-axis. The vector OC projects to ON in the xy-plane and the angle between ON and the x-axis is A. Therefore, the three vectors have components:
 and the explicit expression for
and the explicit expression for  given immediately above
given immediately above
 the spherical sine rule follows immediately. Banerjee [2] provides proofs using elementary linear algebra with the use of projection matrices.
the spherical sine rule follows immediately. Banerjee [2] provides proofs using elementary linear algebra with the use of projection matrices.
 from the third cosine rule:
from the third cosine rule:
 .
Similar techniques with the other two cosine rules give CT3 and CT5.
The other three equations follow by applying rules 1, 3 and 5 to the
polar triangle.
.
Similar techniques with the other two cosine rules give CT3 and CT5.
The other three equations follow by applying rules 1, 3 and 5 to the
polar triangle.
 and
and  ,
,
The proof (Todhunter,[1] Art.49) of the first formula starts from the identity 2sin2(A/2) = 1–cosA, using the cosine rule to express A in terms of the sides and replacing the sum of two cosines by a product. (See sum-to-product identities.) The second formula starts from the identity 2cos2(A/2) = 1+cosA, the third is a quotient and the remainder follow by applying the results to the polar triangle.
Proved by expanding the numerators and using the half angle formulae. (Todhunter,[1] Art.54 and Delambre[3])
These identities follow by division of the Delambre formulae. (Todhunter,[1] Art.52)
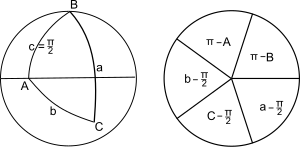
Napier[4] provided an elegant mnemonic aid for the ten independent equations: the mnemonic is called Napier's circle or Napier's pentagon (when the circle in the above figure, right, is replaced by a pentagon).
First write in a circle the six parts of the triangle (three vertex angles, three arc angles for the sides): for the triangle shown above left this gives aCbAcB. Next replace the parts that are not adjacent to C (that is A, c, B) by their complements and then delete the angle C from the list. The remaining parts are as shown in the above figure (right). For any choice of three contiguous parts, one (the middle part) will be adjacent to two parts and opposite the other two parts. The ten Napier's Rules are given by
 we have:
we have:
When one of the sides, say c, of a spherical triangle is equal
to π/2 the corresponding equations are obtained by applying the above
rules to the polar triangle A'B'C' with sides a',b',c' such that A' = π–a, a' = π–A etc. This gives the following equations:
 gives
gives
The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook Spherical trigonometry for the use of colleges and Schools. This book is now readily available on the web.[1] The only significant developments since then have been the application of vector methods for the derivation of the theorems and the use of computers to carry through lengthy calculations.
Contents
Preliminaries
Eight spherical triangles defined by the intersection of three great circles.
Spherical polygons
A spherical polygon on the surface of the sphere is defined by a number of great circle arcs that are the intersection of the surface with planes through the centre of the sphere. Such polygons may have any number of sides. Two planes define a lune, also called a "digon" or bi-angle, the two-sided analogue of the triangle: a familiar example is the curved surface of a segment of an orange. Three planes define a spherical triangle, the principal subject of this article. Four planes define a spherical quadrilateral: such a figure, and higher sided polygons, can always be treated as a number of spherical triangles.From this point the article will be restricted to spherical triangles, denoted simply as triangles.
Notation
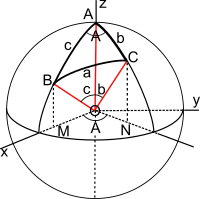
The basic triangle on a unit sphere.
- Both vertices and angles at the vertices are denoted by the same upper case letters A, B and C.
- The angles A, B, C of the triangle are equal to the angles between the planes that intersect the surface of the sphere or, equivalently, the angles between the tangent vectors of the great circle arcs where they meet at the vertices. Angles are in radians. The angles of proper spherical triangles are (by convention) less than π so that π < A + B + C < 3π. (Todhunter,[1] Art.22,32).
- The sides are denoted by lower-case letters a, b, c. On the unit sphere their lengths are numerically equal to the radian measure of the angles that the great circle arcs subtend at the centre. The sides of proper spherical triangles are (by convention) less than π so that 0 < a + b + c < 3π. (Todhunter,[1] Art.22,32).
- The radius of the sphere is taken as unity. For specific practical problems on a sphere of radius R the measured lengths of the sides must be divided by R before using the identities given below. Likewise, after a calculation on the unit sphere the sides a, b, c must be multiplied by R.
Polar triangles
The polar triangle A'B'C'
The triangle A'B'C' is the polar triangle corresponding to triangle ABC. A very important theorem (Todhunter,[1] Art.27) proves that the angles and sides of the polar triangle are given by
Cosine rules and sine rules
Cosine rules
The cosine rule is the fundamental identity of spherical trigonometry: all other identities, including the sine rule, may be derived from the cosine rule. and
and  etc.; see Spherical law of cosines.)
etc.; see Spherical law of cosines.)Sine rules
Derivation of the cosine rule
The spherical cosine formulae were originally proved by elementary geometry and the planar cosine rule (Todhunter,[1] Art.37). He also gives a derivation using simple coordinate geometry and the planar cosine rule (Art.60). The approach outlined here uses simpler vector methods. (These methods are also discussed at Spherical law of cosines.)Consider three unit vectors OA, OB and OC drawn from the origin to the vertices of the triangle (on the unit sphere). The arc BC subtends an angle of magnitude a at the centre and therefore OB·OC=cos a. Introduce a Cartesian basis with OA along the z-axis and OB in the xz-plane making an angle c with the z-axis. The vector OC projects to ON in the xy-plane and the angle between ON and the x-axis is A. Therefore, the three vectors have components:
- OA
OB
OC
.
- OB·OC =
.
Derivation of the sine rule
This derivation is given in Todhunter,[1] (Art.40). From the identity and the explicit expression for
and the explicit expression for  given immediately above
given immediately above the spherical sine rule follows immediately. Banerjee [2] provides proofs using elementary linear algebra with the use of projection matrices.
the spherical sine rule follows immediately. Banerjee [2] provides proofs using elementary linear algebra with the use of projection matrices.Identities
Supplemental cosine rules
Applying the cosine rules to the polar triangle gives (Todhunter,[1] Art.47), i.e. replacing A by π–a, a by π–A etc.,Cotangent four-part formulae
The six parts of a triangle may be written in cyclic order as (aCbAcB). The cotangent, or four-part, formulae relate two sides and two angles forming four consecutive parts around the triangle, for example (aCbA) or (BaCb). In such a set there are inner and outer parts: for example in the set (BaCb) the inner angle is C, the inner side is a, the outer angle is B, the outer side is b. The cotangent rule may be written as (Todhunter,[1] Art.44) from the third cosine rule:
from the third cosine rule: .
Similar techniques with the other two cosine rules give CT3 and CT5.
The other three equations follow by applying rules 1, 3 and 5 to the
polar triangle.
.
Similar techniques with the other two cosine rules give CT3 and CT5.
The other three equations follow by applying rules 1, 3 and 5 to the
polar triangle.Half-angle and half-side formulae
With and
and  ,
,The proof (Todhunter,[1] Art.49) of the first formula starts from the identity 2sin2(A/2) = 1–cosA, using the cosine rule to express A in terms of the sides and replacing the sum of two cosines by a product. (See sum-to-product identities.) The second formula starts from the identity 2cos2(A/2) = 1+cosA, the third is a quotient and the remainder follow by applying the results to the polar triangle.
Delambre (or Gauss) analogies
Proved by expanding the numerators and using the half angle formulae. (Todhunter,[1] Art.54 and Delambre[3])
Napier's analogies
These identities follow by division of the Delambre formulae. (Todhunter,[1] Art.52)
Napier's rules for right spherical triangles
When one of the angles, say C, of a spherical triangle is equal to π/2 the various identities given above are considerably simplified. There are ten identities relating three elements chosen from the set a, b, c, A, B.Napier[4] provided an elegant mnemonic aid for the ten independent equations: the mnemonic is called Napier's circle or Napier's pentagon (when the circle in the above figure, right, is replaced by a pentagon).
First write in a circle the six parts of the triangle (three vertex angles, three arc angles for the sides): for the triangle shown above left this gives aCbAcB. Next replace the parts that are not adjacent to C (that is A, c, B) by their complements and then delete the angle C from the list. The remaining parts are as shown in the above figure (right). For any choice of three contiguous parts, one (the middle part) will be adjacent to two parts and opposite the other two parts. The ten Napier's Rules are given by
-
-
- sine of the middle part = the product of the tangents of the adjacent parts
- sine of the middle part = the product of the cosines of the opposite parts
-
 we have:
we have:Napier's rules for quadrantal triangles
A quadrantal spherical triangle together with Napier's circle for use in his mnemonics
Five-part rules
Substituting the second cosine rule into the first and simplifying gives: gives
gives









![\begin{align}
\sin^2\!A &=1-\left(\frac{\cos a - \cos b\, \cos c}{\sin b \,\sin c}\right)^2\\
&
=\frac{(1-\cos^2\!b)(1-\cos^2\!c)-(\cos a - \cos b\, \cos c)^2}
{\sin^2\!b \,\sin^2\!c}\\
\frac{\sin A}{\sin a}&=\frac{[1-\cos^2\!a-\cos^2\!b-\cos^2\!c+2\cos a\cos b\cos c]^{1/2}}{\sin a\sin b\sin c}.
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/711dd80f0e85c3089c26890701e8f580a3c8c486)




![\begin{array}{lll}
\text{(CT1)}\quad& \cos b\,\cos C=\cot a\,\sin b - \cot A \,\sin C ,\qquad&(aCbA)\\[0ex]
\text{(CT2)}& \cos b\,\cos A=\cot c\,\sin b - \cot C \,\sin A,&(CbAc)\\[0ex]
\text{(CT3)}& \cos c\,\cos A=\cot b\,\sin c - \cot B \,\sin A,&(bAcB)\\[0ex]
\text{(CT4)}& \cos c\,\cos B=\cot a\,\sin c - \cot A \,\sin B,&(AcBa)\\[0ex]
\text{(CT5)}& \cos a\,\cos B=\cot c\,\sin a - \cot C \,\sin B,&(cBaC)\\[0ex]
\text{(CT6)}& \cos a\,\cos C=\cot b\,\sin a - \cot B \,\sin C,&(BaCb).
\end{array}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91c9b85c182d6c68df07addae4d773d511ffba9e)

![\begin{align}
& \sin{\textstyle\frac{1}{2}}A=\left[\frac{\sin(s{-}b)\sin(s{-}c)}{\sin b\sin c}\right]^{1/2}
&\qquad
&\sin{\textstyle\frac{1}{2}}a=\left[\frac{-\cos S\cos (S{-}A)}{\sin B\sin C}\right]^{1/2}\\[2ex]
& \cos{\textstyle\frac{1}{2}}A=\left[\frac{\sin s\sin(s{-}a)}{\sin b\sin c}\right]^{1/2}
&\qquad
&\cos{\textstyle\frac{1}{2}}a=\left[\frac{\cos (S{-}B)\cos (S{-}C)}{\sin B\sin C}\right]^{1/2}\\[2ex]
& \tan{\textstyle\frac{1}{2}}A=\left[\frac{\sin(s{-}b)\sin(s{-}c)}{\sin s\sin(s{-}a)}\right]^{1/2}
&\qquad
&\tan{\textstyle\frac{1}{2}}a=\left[\frac{-\cos S\cos (S{-}A)}{\cos (S{-}B)\cos(S{-}C)}\right]^{1/2}
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac0513fa1055a5a7ca83869be30d2d006a29e4b1)
![\begin{align}
&\\
\frac{\sin{\textstyle\frac{1}{2}}(A{+}B)}
{\cos{\textstyle\frac{1}{2}}C}
=\frac{\cos{\textstyle\frac{1}{2}}(a{-}b)}
{\cos{\textstyle\frac{1}{2}}c}
&\qquad\qquad
&
\frac{\sin{\textstyle\frac{1}{2}}(A{-}B)}
{\cos{\textstyle\frac{1}{2}}C}
=\frac{\sin{\textstyle\frac{1}{2}}(a{-}b)}
{\sin{\textstyle\frac{1}{2}}c}
\\[2ex]
\frac{\cos{\textstyle\frac{1}{2}}(A{+}B)}
{\sin{\textstyle\frac{1}{2}}C}
=\frac{\cos{\textstyle\frac{1}{2}}(a{+}b)}
{\cos{\textstyle\frac{1}{2}}c}
&\qquad
&
\frac{\cos{\textstyle\frac{1}{2}}(A{-}B)}
{\sin{\textstyle\frac{1}{2}}C}
=\frac{\sin{\textstyle\frac{1}{2}}(a{+}b)}
{\sin{\textstyle\frac{1}{2}}c}
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5d2569d8cff215686f38a036b0070d2c4a2f878)
![\begin{align}
&&\\[-2ex]\displaystyle
{\tan{\textstyle\frac{1}{2}}(A{+}B)}
=\frac{\cos{\textstyle\frac{1}{2}}(a{-}b)}
{\cos{\textstyle\frac{1}{2}}(a{+}b)}
\cot{\textstyle\frac{1}{2}C}
&\qquad
&
{\tan{\textstyle\frac{1}{2}}(a{+}b)}
=\frac{\cos{\textstyle\frac{1}{2}}(A{-}B)}
{\cos{\textstyle\frac{1}{2}}(A{+}B)}
\tan{\textstyle\frac{1}{2}c}
\\[2ex]
{\tan{\textstyle\frac{1}{2}}(A{-}B)}
=\frac{\sin{\textstyle\frac{1}{2}}(a{-}b)}
{\sin{\textstyle\frac{1}{2}}(a{+}b)}
\cot{\textstyle\frac{1}{2}C}
&\qquad
& {\tan{\textstyle\frac{1}{2}}(a{-}b)}
=\frac{\sin{\textstyle\frac{1}{2}}(A{-}B)}
{\sin{\textstyle\frac{1}{2}}(A{+}B)}
\tan{\textstyle\frac{1}{2}c}
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/147400666fc0d9f657547bfaefa17a527c014d0f)







No comments:
Post a Comment