😊 THANKYOU😊
Sunday, 29 January 2017
Thursday, 26 January 2017
Birth Of Trigonometry
The complex origins of trigonometry
are embedded in the history of the simple word "sine,"
a mistranslation of an Arabic transliteration of a Sanskrit mathematical
term! The complex etymology of "sine" reveals trigonometry's
roots in Babylonian, Greek, Hellenistic, Indian, and Arabic mathematics
and astronomy.
 Although trigonometry now is usually taught
beginning with plane triangles, its origins lie in the world of
astronomy and spherical triangles. Before the sixteenth century,
astronomy was based on the notion that the earth stood at the
center of a series of nested spheres. To calculate the positions
of stars or planets, one needed to use concepts we now refer to
as trigonometry.
Although trigonometry now is usually taught
beginning with plane triangles, its origins lie in the world of
astronomy and spherical triangles. Before the sixteenth century,
astronomy was based on the notion that the earth stood at the
center of a series of nested spheres. To calculate the positions
of stars or planets, one needed to use concepts we now refer to
as trigonometry.
The earliest uses of trigonometric functions were related to the chords of a circle, and the recognition that the length of the chord subtended by a given angle x was (in modern terms) 2sin(x/2). The Greek astronomer and mathematician Hipparchus produced the first known table of chords in 140 BC. His work was further developed by astronomers Menelaus (ca. AD 100) and Ptolemy (ca. AD 100), who relied on Babylonian observations and traditions.
Babylonian and Greek influences mingled with rich native mathematical developments in India around AD 500 to produce a trigonometry closer to its modern form. Hindu mathematical works such as that of Aryabhata give tables of half chords, known by the term jya-ardha or simply jya, which bears the following relationship to our modern concept of sine: jya x = r sinx, as illustrated below.
 Jya here represents the
half chord AM.
Jya here represents the
half chord AM.
From India the sine function was introduced to the Arab world in the 8th century, where the term jya was transliterated into jiba or jyb. Early Latin translations of Arabic mathematical treatises mistook jiba for the Arabic word jaib, which can mean the opening of a woman's garment at the neck. Accordingly, jaib was translated into the Latin sinus, which can mean "fold" (in a garment), "bosom," "bay," or even "curve." Hence our word "sine."
Another set of trigonometric functions, tangent and cotangent, developed from the study of the lengths of shadows cast by objects of various heights. Thales of Miletus used shadow lenghts to calculate the heights of the pyramids in around 600 BC. Both Indian and Arabic mathematics developed a trigonometric tradition based on shadow lengths, a tradition that, in turn, influenced European mathematics. Click here for an applet illustrating sticks and shadows. (You can follow the links to move through illustrations of basic trigonometry functions, including the use of the tangent function for surveying.)
The functions secant and cosecant derive from tables first used by navigators in the fifteenth century.
As for the word "trigonometry," it first appeared as the title of a book Trigonometria (literally, the measuring of triangles), published by Bartholomeo Pitiscus in 1595.
The earliest uses of trigonometric functions were related to the chords of a circle, and the recognition that the length of the chord subtended by a given angle x was (in modern terms) 2sin(x/2). The Greek astronomer and mathematician Hipparchus produced the first known table of chords in 140 BC. His work was further developed by astronomers Menelaus (ca. AD 100) and Ptolemy (ca. AD 100), who relied on Babylonian observations and traditions.
Babylonian and Greek influences mingled with rich native mathematical developments in India around AD 500 to produce a trigonometry closer to its modern form. Hindu mathematical works such as that of Aryabhata give tables of half chords, known by the term jya-ardha or simply jya, which bears the following relationship to our modern concept of sine: jya x = r sinx, as illustrated below.
From India the sine function was introduced to the Arab world in the 8th century, where the term jya was transliterated into jiba or jyb. Early Latin translations of Arabic mathematical treatises mistook jiba for the Arabic word jaib, which can mean the opening of a woman's garment at the neck. Accordingly, jaib was translated into the Latin sinus, which can mean "fold" (in a garment), "bosom," "bay," or even "curve." Hence our word "sine."
Another set of trigonometric functions, tangent and cotangent, developed from the study of the lengths of shadows cast by objects of various heights. Thales of Miletus used shadow lenghts to calculate the heights of the pyramids in around 600 BC. Both Indian and Arabic mathematics developed a trigonometric tradition based on shadow lengths, a tradition that, in turn, influenced European mathematics. Click here for an applet illustrating sticks and shadows. (You can follow the links to move through illustrations of basic trigonometry functions, including the use of the tangent function for surveying.)
The functions secant and cosecant derive from tables first used by navigators in the fifteenth century.
As for the word "trigonometry," it first appeared as the title of a book Trigonometria (literally, the measuring of triangles), published by Bartholomeo Pitiscus in 1595.
Father of Trigonometry
Hipparchus
| Hipparchus | |
|---|---|
 |
|
| Born | c. 190 BC Nicaea, Kingdom of Bithynia |
| Died | c. 120 BC Rhodes, Roman Republic |
| Occupation | |
Hipparchus was born in Nicaea, Bithynia (now Iznik, Turkey), and probably died on the island of Rhodes. He is known to have been a working astronomer at least from 162 to 127 BC.[3] Hipparchus is considered the greatest ancient astronomical observer and, by some, the greatest overall astronomer of antiquity. He was the first whose quantitative and accurate models for the motion of the Sun and Moon survive. For this he certainly made use of the observations and perhaps the mathematical techniques accumulated over centuries by the Babylonians and other people from Mesopotamia. He developed trigonometry and constructed trigonometric tables, and he solved several problems of spherical trigonometry. With his solar and lunar theories and his trigonometry, he may have been the first to develop a reliable method to predict solar eclipses. His other reputed achievements include the discovery and measurement of Earth's precession, the compilation of the first comprehensive star catalog of the western world, and possibly the invention of the astrolabe, also of the armillary sphere, which he used during the creation of much of the star catalogue.
Contents
Life and work
Relatively little of Hipparchus's direct work survives into modern times. Although he wrote at least fourteen books, only his commentary on the popular astronomical poem by Aratus was preserved by later copyists. Most of what is known about Hipparchus comes from Strabo's Geography and Pliny's Natural History in the 1st century; Ptolemy's 2nd-century Almagest; and additional references to him in the 4th century by Pappus of Alexandria and Theon of Alexandria in their commentaries on the Almagest.[4]There is a strong tradition that Hipparchus was born in Nicaea (Greek Νίκαια), in the ancient district of Bithynia (modern-day Iznik in province Bursa), in what today is the country Turkey.
The exact dates of his life are not known, but Ptolemy attributes to him astronomical observations in the period from 147–127 BC, and some of these are stated as made in Rhodes; earlier observations since 162 BC might also have been made by him. His birth date (c. 190 BC) was calculated by Delambre based on clues in his work. Hipparchus must have lived some time after 127 BC because he analyzed and published his observations from that year. Hipparchus obtained information from Alexandria as well as Babylon, but it is not known when or if he visited these places. He is believed to have died on the island of Rhodes, where he seems to have spent most of his later life.
It is not known what Hipparchus's economic means were nor how he supported his scientific activities. His appearance is likewise unknown: there are no contemporary portraits. In the 2nd and 3rd centuries coins were made in his honour in Bithynia that bear his name and show him with a globe; this supports the tradition that he was born there.
Hipparchus is thought to be the first to calculate a heliocentric system,[5] but he abandoned his work because the calculations showed the orbits were not perfectly circular as believed to be mandatory by the science of the time. As an astronomer of antiquity his influence, supported by ideas from Aristotle, held sway for nearly 2000 years, until the heliocentric model of Copernicus.
Hipparchus's only preserved work is Τῶν Ἀράτου καὶ Εὐδόξου φαινομένων ἐξήγησις ("Commentary on the Phaenomena of Eudoxus and Aratus"). This is a highly critical commentary in the form of two books on a popular poem by Aratus based on the work by Eudoxus.[6] Hipparchus also made a list of his major works, which apparently mentioned about fourteen books, but which is only known from references by later authors. His famous star catalog was incorporated into the one by Ptolemy, and may be almost perfectly reconstructed by subtraction of two and two thirds degrees from the longitudes of Ptolemy's stars. The first trigonometric table was apparently compiled by Hipparchus, who is now consequently known as "the father of trigonometry".
Modern speculation
Hipparchus was in the international news in 2005, when it was again proposed (as in 1898) that the data on the celestial globe of Hipparchus or in his star catalog may have been preserved in the only surviving large ancient celestial globe which depicts the constellations with moderate accuracy, the globe carried by the Farnese Atlas. There are a variety of mis-steps[7] in the more ambitious 2005 paper, thus no specialists in the area accept its widely publicized speculation.[8]Lucio Russo has said that Plutarch, in his work On the Face in the Moon, was reporting some physical theories that we consider to be Newtonian and that these may have come originally from Hipparchus;[9] he goes on to say that Newton may have been influenced by them.[10] According to one book review, both of these claims have been rejected by other scholars.[11]
A line in Plutarch's Table Talk states that Hipparchus counted 103049 compound propositions that can be formed from ten simple propositions. 103049 is the tenth Schröder–Hipparchus number, which counts the number of ways of adding one or more pairs of parentheses around consecutive subsequences of two or more items in any sequence of ten symbols. This has led to speculation that Hipparchus knew about enumerative combinatorics, a field of mathematics that developed independently in modern mathematics.[12][13]
Babylonian sources
Further information: Babylonian astronomy
Earlier Greek astronomers and mathematicians were influenced by
Babylonian astronomy to some extent, for instance the period relations
of the Metonic cycle and Saros cycle may have come from Babylonian sources (see "Babylonian astronomical diaries"). Hipparchus seems to have been the first to exploit Babylonian astronomical knowledge and techniques systematically.[14] Except for Timocharis and Aristillus, he was the first Greek known to divide the circle in 360 degrees of 60 arc minutes (Eratosthenes before him used a simpler sexagesimal system dividing a circle into 60 parts). He also used the Babylonian unit pechus ("cubit") of about 2° or 2.5°.Hipparchus probably compiled a list of Babylonian astronomical observations; G. J. Toomer, a historian of astronomy, has suggested that Ptolemy's knowledge of eclipse records and other Babylonian observations in the Almagest came from a list made by Hipparchus. Hipparchus's use of Babylonian sources has always been known in a general way, because of Ptolemy's statements. However, Franz Xaver Kugler demonstrated that the synodic and anomalistic periods that Ptolemy attributes to Hipparchus had already been used in Babylonian ephemerides, specifically the collection of texts nowadays called "System B" (sometimes attributed to Kidinnu).[15]
Hipparchus's long draconitic lunar period (5458 months = 5923 lunar nodal periods) also appears a few times in Babylonian records.[16] But the only such tablet explicitly dated is post-Hipparchus so the direction of transmission is not settled by the tablets.
Hipparchus's draconitic lunar motion cannot be solved by the lunar-four arguments that are sometimes proposed to explain his anomalistic motion. A solution that has produced the exact 5458/5923 ratio is rejected by most historians though it uses the only anciently attested method of determining such ratios, and it automatically delivers the ratio's four-digit numerator and denominator. Hipparchus initially used (Almagest 6.9) his 141 B. C. E. eclipse with a Babylonian eclipse of 720 B. C. E. to find the less accurate ratio 7160 synodic months = 7770 draconitic months, simplified by him to 716 = 777 through division by 10. (He similarly found from the 345-year cycle the ratio 4267 synodic months = 4573 anomalistic months and divided by 17 to obtain the standard ratio 251 synodic months = 269 anomalistic months.) If he sought a longer time base for this draconitic investigation he could use his same 141 B. C. E. eclipse with a moonrise 1245 B. C. E. eclipse from Babylon, an interval of 13645 synodic months = 148807 1/2 draconitic months ≈ 14623 1/2 anomalistic months. Dividing by 5/2 produces 5458 synodic months = 5923 precisely.[17] The obvious main objection is that the early eclipse is unattested though that is not surprising in itself and there is no consensus on whether Babylonian observations were recorded this remotely. Though Hipparchus's tables formally went back only to 747 B. C. E., 600 years before his era, the tables were actually good back to before the eclipse in question because as only recently noted[18] their use in reverse is no more difficult than forwards.
Geometry, trigonometry, and other mathematical techniques
Hipparchus was recognized as the first mathematician known to have possessed a trigonometric table, which he needed when computing the eccentricity of the orbits of the Moon and Sun. He tabulated values for the chord function, which gives the length of the chord for each angle. He did this for a circle with a circumference of 21600 and a radius (rounded) of 3438 units: this circle has a unit length of 1 arc minute along its perimeter. He tabulated the chords for angles with increments of 7.5°. In modern terms, the chord of an angle equals the radius times twice the sine of half of the angle, i.e.:- chord(A) = r(2 sin(A/2)).
For his chord table Hipparchus must have used a better approximation for π than the one from Archimedes of between 3 + 1/7 and 3 + 10/71; perhaps he had the one later used by Ptolemy: 3;8:30 (sexagesimal) (Almagest VI.7); but it is not known if he computed an improved value himself.
But some scholars do not believe Arayabhatta's Sin table has anything to do with Hipparchus's chord table which does not exist today. Some scholars do not agree with this hypothesis that Hipparchus constructed a chord table. Bo. C Klintberg states "With mathematical reconstructions and philosophical arguments I show that Toomer's 1973 paper never contained any conclusive evidence for his claims that Hipparchus had a 3438'-based chord table, and that the Indians used that table to compute their sine tables. Recalculating Toomer's reconstructions with a 3600' radius – i.e. the radius of the chord table in Ptolemy's Almagest, expressed in 'minutes' instead of 'degrees' – generates Hipparchan-like ratios similar to those produced by a 3438' radius. It is therefore possible that the radius of Hipparchus's chord table was 3600', and that the Indians independently constructed their 3438'-based sine table." [20]
Hipparchus could construct his chord table using the Pythagorean theorem and a theorem known to Archimedes. He also might have developed and used the theorem in plane geometry called Ptolemy's theorem, because it was proved by Ptolemy in his Almagest (I.10) (later elaborated on by Carnot).
Hipparchus was the first to show that the stereographic projection is conformal, and that it transforms circles on the sphere that do not pass through the center of projection to circles on the plane. This was the basis for the astrolabe.
Besides geometry, Hipparchus also used arithmetic techniques developed by the Chaldeans. He was one of the first Greek mathematicians to do this, and in this way expanded the techniques available to astronomers and geographers.
There are several indications that Hipparchus knew spherical trigonometry, but the first surviving text of it is that of Menelaus of Alexandria in the 1st century, who on that basis is now commonly credited with its discovery. (Previous to the finding of the proofs of Menelaus a century ago, Ptolemy was credited with the invention of spherical trigonometry.) Ptolemy later used spherical trigonometry to compute things like the rising and setting points of the ecliptic, or to take account of the lunar parallax. Hipparchus may have used a globe for these tasks, reading values off coordinate grids drawn on it, or he may have made approximations from planar geometry, or perhaps used arithmetical approximations developed by the Chaldeans. He might have used spherical trigonometry.
Aubrey Diller has shown that the clima calculations which Strabo preserved from Hipparchus were performed by spherical trigonometry with the sole accurate obliquity known to have been used by ancient astronomers, 23°40'. All thirteen clima figures agree with Diller's proposal.[21] Further confirming his contention is the finding that the big errors in Hipparchus's longitude of Regulus and both longitudes of Spica agree to a few minutes in all three instances with a theory that he took the wrong sign for his correction for parallax when using eclipses for determining stars' positions.
How Trigonometry Used In Physics
How is trigonometry used in physics?
A:
Quick Answer
Because it has such a strong ability to explain space and the relationships between angles, trigonometry is used in almost every branch of modern physics, according to Clark University. Any field of physics that includes the use of angles or sides uses trigonometry. Some of the first fields in physics, statics and optics relied heavily on trigonometry during their pioneering stages.Full Answer
Trigonometry is the mathematical science that studies the relationships between lengths and angles of triangles. However, it has applications that extend to such shapes as circles, spheres and other three-dimensional geometric constructs. Because of this, trigonometry is incredibly useful in understanding and modeling the real world. Certain constructs, such as suspended crates and pulley systems, can be described with series of angles and lines. Some applications of trigonometry include those with angular momentum and movement up or down inclines.Trigonometry is also vital to the understanding of light rays and how they behave. Because complex problems, such as the bending of a light as it passes through glass, can be broken down into mathematical components, they can be solved and analyzed with trigonometric methods. Angles of incidence and refraction inside of triangular prisms can be solved for with trigonometry. Physicists can use information like this to estimate the refractive indexes of certain materials.
Plane Trigonometry
Q:
What is the definition of "plane trigonometry"?
A:
Quick Answer
"Plane trigonometry" is a branch of mathematics that focuses on the relationship between the sides and angles of a triangle. Plane trigonometry builds upon the basic concepts of Euclidean geometry, and it has applications in a variety of mathematical fields, from physics to advanced calculus.
Credit:
Stockbyte
Stockbyte
Getty Images
Full Answer
Celestial navigator Eric DeMan explains that plane trigonometry examines the vertices of a triangle and the surfaces of the planes that cover its three unique sides. Since triangles are composed of straight lines, understanding the relationship between the angles that make up a triangle is essential to understanding plane trigonometry.The Encyclopaedia Britannica further defines plane trigonometry as an attempt to deduce the remaining sides of a triangle from the sides that are known. While this may seem like the definition of trigonometry, plane trigonometry takes the concept to a higher level of understanding. Traditional geometry only explains the nature of triangles that follow the basic rules of the Euclidean plane. Plane trigonometry goes beyond the Euclidean plane, explaining the nature of more complex relationships between triangles. Plane trigonometry works entirely through logic and deduction, inferring one set of facts about a given triangle based on what is known about the triangle's other angles, vertices and planes.
Spherical Trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the relationships between trigonometric functions of the sides and angles of the spherical polygons (especially spherical triangles) defined by a number of intersecting great circles on the sphere. Spherical trigonometry is of great importance for calculations in astronomy, geodesy and navigation.
The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook Spherical trigonometry for the use of colleges and Schools. This book is now readily available on the web.[1] The only significant developments since then have been the application of vector methods for the derivation of the theorems and the use of computers to carry through lengthy calculations.
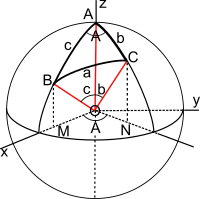
From this point the article will be restricted to spherical triangles, denoted simply as triangles.
The polar triangle associated with a triangle ABC is defined as
follows. Consider the great circle that contains the side BC. This great
circle is defined by the intersection of a diametral plane with the
surface. Draw the normal to that plane at the centre: it intersects the
surface at two points and the point that is on the same side of the
plane as A is (conventionally) termed the pole of A and it is denoted by
A'. The points B' and C' are defined similarly.
The triangle A'B'C' is the polar triangle corresponding to triangle ABC. A very important theorem (Todhunter,[1] Art.27) proves that the angles and sides of the polar triangle are given by
 and
and  etc.; see Spherical law of cosines.)
etc.; see Spherical law of cosines.)
Consider three unit vectors OA, OB and OC drawn from the origin to the vertices of the triangle (on the unit sphere). The arc BC subtends an angle of magnitude a at the centre and therefore OB·OC=cos a. Introduce a Cartesian basis with OA along the z-axis and OB in the xz-plane making an angle c with the z-axis. The vector OC projects to ON in the xy-plane and the angle between ON and the x-axis is A. Therefore, the three vectors have components:
 and the explicit expression for
and the explicit expression for  given immediately above
given immediately above
 the spherical sine rule follows immediately. Banerjee [2] provides proofs using elementary linear algebra with the use of projection matrices.
the spherical sine rule follows immediately. Banerjee [2] provides proofs using elementary linear algebra with the use of projection matrices.
 from the third cosine rule:
from the third cosine rule:
 .
Similar techniques with the other two cosine rules give CT3 and CT5.
The other three equations follow by applying rules 1, 3 and 5 to the
polar triangle.
.
Similar techniques with the other two cosine rules give CT3 and CT5.
The other three equations follow by applying rules 1, 3 and 5 to the
polar triangle.
 and
and  ,
,
The proof (Todhunter,[1] Art.49) of the first formula starts from the identity 2sin2(A/2) = 1–cosA, using the cosine rule to express A in terms of the sides and replacing the sum of two cosines by a product. (See sum-to-product identities.) The second formula starts from the identity 2cos2(A/2) = 1+cosA, the third is a quotient and the remainder follow by applying the results to the polar triangle.
Proved by expanding the numerators and using the half angle formulae. (Todhunter,[1] Art.54 and Delambre[3])
These identities follow by division of the Delambre formulae. (Todhunter,[1] Art.52)
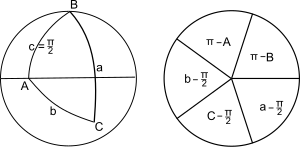
Napier[4] provided an elegant mnemonic aid for the ten independent equations: the mnemonic is called Napier's circle or Napier's pentagon (when the circle in the above figure, right, is replaced by a pentagon).
First write in a circle the six parts of the triangle (three vertex angles, three arc angles for the sides): for the triangle shown above left this gives aCbAcB. Next replace the parts that are not adjacent to C (that is A, c, B) by their complements and then delete the angle C from the list. The remaining parts are as shown in the above figure (right). For any choice of three contiguous parts, one (the middle part) will be adjacent to two parts and opposite the other two parts. The ten Napier's Rules are given by
 we have:
we have:
When one of the sides, say c, of a spherical triangle is equal
to π/2 the corresponding equations are obtained by applying the above
rules to the polar triangle A'B'C' with sides a',b',c' such that A' = π–a, a' = π–A etc. This gives the following equations:
 gives
gives
The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook Spherical trigonometry for the use of colleges and Schools. This book is now readily available on the web.[1] The only significant developments since then have been the application of vector methods for the derivation of the theorems and the use of computers to carry through lengthy calculations.
Contents
Preliminaries
Eight spherical triangles defined by the intersection of three great circles.
Spherical polygons
A spherical polygon on the surface of the sphere is defined by a number of great circle arcs that are the intersection of the surface with planes through the centre of the sphere. Such polygons may have any number of sides. Two planes define a lune, also called a "digon" or bi-angle, the two-sided analogue of the triangle: a familiar example is the curved surface of a segment of an orange. Three planes define a spherical triangle, the principal subject of this article. Four planes define a spherical quadrilateral: such a figure, and higher sided polygons, can always be treated as a number of spherical triangles.From this point the article will be restricted to spherical triangles, denoted simply as triangles.
Notation
The basic triangle on a unit sphere.
- Both vertices and angles at the vertices are denoted by the same upper case letters A, B and C.
- The angles A, B, C of the triangle are equal to the angles between the planes that intersect the surface of the sphere or, equivalently, the angles between the tangent vectors of the great circle arcs where they meet at the vertices. Angles are in radians. The angles of proper spherical triangles are (by convention) less than π so that π < A + B + C < 3π. (Todhunter,[1] Art.22,32).
- The sides are denoted by lower-case letters a, b, c. On the unit sphere their lengths are numerically equal to the radian measure of the angles that the great circle arcs subtend at the centre. The sides of proper spherical triangles are (by convention) less than π so that 0 < a + b + c < 3π. (Todhunter,[1] Art.22,32).
- The radius of the sphere is taken as unity. For specific practical problems on a sphere of radius R the measured lengths of the sides must be divided by R before using the identities given below. Likewise, after a calculation on the unit sphere the sides a, b, c must be multiplied by R.
Polar triangles
The polar triangle A'B'C'
The triangle A'B'C' is the polar triangle corresponding to triangle ABC. A very important theorem (Todhunter,[1] Art.27) proves that the angles and sides of the polar triangle are given by
Cosine rules and sine rules
Cosine rules
The cosine rule is the fundamental identity of spherical trigonometry: all other identities, including the sine rule, may be derived from the cosine rule. and
and  etc.; see Spherical law of cosines.)
etc.; see Spherical law of cosines.)Sine rules
Derivation of the cosine rule
The spherical cosine formulae were originally proved by elementary geometry and the planar cosine rule (Todhunter,[1] Art.37). He also gives a derivation using simple coordinate geometry and the planar cosine rule (Art.60). The approach outlined here uses simpler vector methods. (These methods are also discussed at Spherical law of cosines.)Consider three unit vectors OA, OB and OC drawn from the origin to the vertices of the triangle (on the unit sphere). The arc BC subtends an angle of magnitude a at the centre and therefore OB·OC=cos a. Introduce a Cartesian basis with OA along the z-axis and OB in the xz-plane making an angle c with the z-axis. The vector OC projects to ON in the xy-plane and the angle between ON and the x-axis is A. Therefore, the three vectors have components:
- OA
OB
OC
.
- OB·OC =
.
Derivation of the sine rule
This derivation is given in Todhunter,[1] (Art.40). From the identity and the explicit expression for
and the explicit expression for  given immediately above
given immediately above the spherical sine rule follows immediately. Banerjee [2] provides proofs using elementary linear algebra with the use of projection matrices.
the spherical sine rule follows immediately. Banerjee [2] provides proofs using elementary linear algebra with the use of projection matrices.Identities
Supplemental cosine rules
Applying the cosine rules to the polar triangle gives (Todhunter,[1] Art.47), i.e. replacing A by π–a, a by π–A etc.,Cotangent four-part formulae
The six parts of a triangle may be written in cyclic order as (aCbAcB). The cotangent, or four-part, formulae relate two sides and two angles forming four consecutive parts around the triangle, for example (aCbA) or (BaCb). In such a set there are inner and outer parts: for example in the set (BaCb) the inner angle is C, the inner side is a, the outer angle is B, the outer side is b. The cotangent rule may be written as (Todhunter,[1] Art.44) from the third cosine rule:
from the third cosine rule: .
Similar techniques with the other two cosine rules give CT3 and CT5.
The other three equations follow by applying rules 1, 3 and 5 to the
polar triangle.
.
Similar techniques with the other two cosine rules give CT3 and CT5.
The other three equations follow by applying rules 1, 3 and 5 to the
polar triangle.Half-angle and half-side formulae
With and
and  ,
,The proof (Todhunter,[1] Art.49) of the first formula starts from the identity 2sin2(A/2) = 1–cosA, using the cosine rule to express A in terms of the sides and replacing the sum of two cosines by a product. (See sum-to-product identities.) The second formula starts from the identity 2cos2(A/2) = 1+cosA, the third is a quotient and the remainder follow by applying the results to the polar triangle.
Delambre (or Gauss) analogies
Proved by expanding the numerators and using the half angle formulae. (Todhunter,[1] Art.54 and Delambre[3])
Napier's analogies
These identities follow by division of the Delambre formulae. (Todhunter,[1] Art.52)
Napier's rules for right spherical triangles
When one of the angles, say C, of a spherical triangle is equal to π/2 the various identities given above are considerably simplified. There are ten identities relating three elements chosen from the set a, b, c, A, B.Napier[4] provided an elegant mnemonic aid for the ten independent equations: the mnemonic is called Napier's circle or Napier's pentagon (when the circle in the above figure, right, is replaced by a pentagon).
First write in a circle the six parts of the triangle (three vertex angles, three arc angles for the sides): for the triangle shown above left this gives aCbAcB. Next replace the parts that are not adjacent to C (that is A, c, B) by their complements and then delete the angle C from the list. The remaining parts are as shown in the above figure (right). For any choice of three contiguous parts, one (the middle part) will be adjacent to two parts and opposite the other two parts. The ten Napier's Rules are given by
-
-
- sine of the middle part = the product of the tangents of the adjacent parts
- sine of the middle part = the product of the cosines of the opposite parts
-
 we have:
we have:Napier's rules for quadrantal triangles
A quadrantal spherical triangle together with Napier's circle for use in his mnemonics
Five-part rules
Substituting the second cosine rule into the first and simplifying gives: gives
gives
Subscribe to:
Comments (Atom)












![\begin{align}
\sin^2\!A &=1-\left(\frac{\cos a - \cos b\, \cos c}{\sin b \,\sin c}\right)^2\\
&
=\frac{(1-\cos^2\!b)(1-\cos^2\!c)-(\cos a - \cos b\, \cos c)^2}
{\sin^2\!b \,\sin^2\!c}\\
\frac{\sin A}{\sin a}&=\frac{[1-\cos^2\!a-\cos^2\!b-\cos^2\!c+2\cos a\cos b\cos c]^{1/2}}{\sin a\sin b\sin c}.
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/711dd80f0e85c3089c26890701e8f580a3c8c486)




![\begin{array}{lll}
\text{(CT1)}\quad& \cos b\,\cos C=\cot a\,\sin b - \cot A \,\sin C ,\qquad&(aCbA)\\[0ex]
\text{(CT2)}& \cos b\,\cos A=\cot c\,\sin b - \cot C \,\sin A,&(CbAc)\\[0ex]
\text{(CT3)}& \cos c\,\cos A=\cot b\,\sin c - \cot B \,\sin A,&(bAcB)\\[0ex]
\text{(CT4)}& \cos c\,\cos B=\cot a\,\sin c - \cot A \,\sin B,&(AcBa)\\[0ex]
\text{(CT5)}& \cos a\,\cos B=\cot c\,\sin a - \cot C \,\sin B,&(cBaC)\\[0ex]
\text{(CT6)}& \cos a\,\cos C=\cot b\,\sin a - \cot B \,\sin C,&(BaCb).
\end{array}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91c9b85c182d6c68df07addae4d773d511ffba9e)

![\begin{align}
& \sin{\textstyle\frac{1}{2}}A=\left[\frac{\sin(s{-}b)\sin(s{-}c)}{\sin b\sin c}\right]^{1/2}
&\qquad
&\sin{\textstyle\frac{1}{2}}a=\left[\frac{-\cos S\cos (S{-}A)}{\sin B\sin C}\right]^{1/2}\\[2ex]
& \cos{\textstyle\frac{1}{2}}A=\left[\frac{\sin s\sin(s{-}a)}{\sin b\sin c}\right]^{1/2}
&\qquad
&\cos{\textstyle\frac{1}{2}}a=\left[\frac{\cos (S{-}B)\cos (S{-}C)}{\sin B\sin C}\right]^{1/2}\\[2ex]
& \tan{\textstyle\frac{1}{2}}A=\left[\frac{\sin(s{-}b)\sin(s{-}c)}{\sin s\sin(s{-}a)}\right]^{1/2}
&\qquad
&\tan{\textstyle\frac{1}{2}}a=\left[\frac{-\cos S\cos (S{-}A)}{\cos (S{-}B)\cos(S{-}C)}\right]^{1/2}
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac0513fa1055a5a7ca83869be30d2d006a29e4b1)
![\begin{align}
&\\
\frac{\sin{\textstyle\frac{1}{2}}(A{+}B)}
{\cos{\textstyle\frac{1}{2}}C}
=\frac{\cos{\textstyle\frac{1}{2}}(a{-}b)}
{\cos{\textstyle\frac{1}{2}}c}
&\qquad\qquad
&
\frac{\sin{\textstyle\frac{1}{2}}(A{-}B)}
{\cos{\textstyle\frac{1}{2}}C}
=\frac{\sin{\textstyle\frac{1}{2}}(a{-}b)}
{\sin{\textstyle\frac{1}{2}}c}
\\[2ex]
\frac{\cos{\textstyle\frac{1}{2}}(A{+}B)}
{\sin{\textstyle\frac{1}{2}}C}
=\frac{\cos{\textstyle\frac{1}{2}}(a{+}b)}
{\cos{\textstyle\frac{1}{2}}c}
&\qquad
&
\frac{\cos{\textstyle\frac{1}{2}}(A{-}B)}
{\sin{\textstyle\frac{1}{2}}C}
=\frac{\sin{\textstyle\frac{1}{2}}(a{+}b)}
{\sin{\textstyle\frac{1}{2}}c}
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5d2569d8cff215686f38a036b0070d2c4a2f878)
![\begin{align}
&&\\[-2ex]\displaystyle
{\tan{\textstyle\frac{1}{2}}(A{+}B)}
=\frac{\cos{\textstyle\frac{1}{2}}(a{-}b)}
{\cos{\textstyle\frac{1}{2}}(a{+}b)}
\cot{\textstyle\frac{1}{2}C}
&\qquad
&
{\tan{\textstyle\frac{1}{2}}(a{+}b)}
=\frac{\cos{\textstyle\frac{1}{2}}(A{-}B)}
{\cos{\textstyle\frac{1}{2}}(A{+}B)}
\tan{\textstyle\frac{1}{2}c}
\\[2ex]
{\tan{\textstyle\frac{1}{2}}(A{-}B)}
=\frac{\sin{\textstyle\frac{1}{2}}(a{-}b)}
{\sin{\textstyle\frac{1}{2}}(a{+}b)}
\cot{\textstyle\frac{1}{2}C}
&\qquad
& {\tan{\textstyle\frac{1}{2}}(a{-}b)}
=\frac{\sin{\textstyle\frac{1}{2}}(A{-}B)}
{\sin{\textstyle\frac{1}{2}}(A{+}B)}
\tan{\textstyle\frac{1}{2}c}
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/147400666fc0d9f657547bfaefa17a527c014d0f)